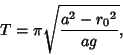Find the tunnel between two points 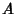 and
and 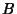 on a gravitating Sphere which gives the shortest transit time under the
force of gravity.
on a gravitating Sphere which gives the shortest transit time under the
force of gravity.  Assume the Sphere to be nonrotating, of Radius
Assume the Sphere to be nonrotating, of Radius 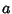 , and with
uniform density
, and with
uniform density 
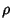 . Then the standard form Euler-Lagrange Differential Equation in polar
coordinates is
. Then the standard form Euler-Lagrange Differential Equation in polar
coordinates is
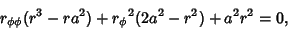 |
(1) |
along with the boundary conditions 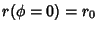 ,
,
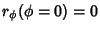 ,
,
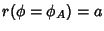 , and
, and
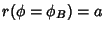 .
Integrating once gives
.
Integrating once gives
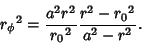 |
(2) |
But this is the equation of a Hypocycloid generated by a Circle of Radius
 rolling
inside the Circle of Radius
rolling
inside the Circle of Radius 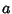 , so the tunnel is shaped like an arc of a Hypocycloid. The transit time
from point
, so the tunnel is shaped like an arc of a Hypocycloid. The transit time
from point 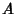 to point
to point 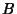 is
is
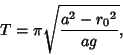 |
(3) |
where
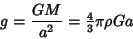 |
(4) |
is the surface gravity with 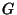 the universal gravitational constant.
the universal gravitational constant. 
© 1996-9 Eric W. Weisstein
1999-05-26
![]() and
and ![]() on a gravitating Sphere which gives the shortest transit time under the
force of gravity.
on a gravitating Sphere which gives the shortest transit time under the
force of gravity. ![]() Assume the Sphere to be nonrotating, of Radius
Assume the Sphere to be nonrotating, of Radius ![]() , and with
uniform density
, and with
uniform density ![]()
![]() . Then the standard form Euler-Lagrange Differential Equation in polar
coordinates is
. Then the standard form Euler-Lagrange Differential Equation in polar
coordinates is