|
|
|
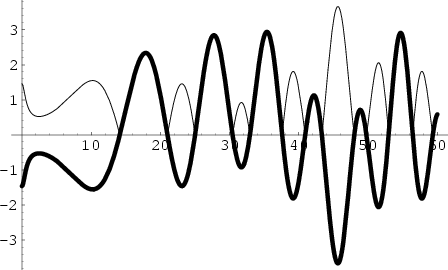
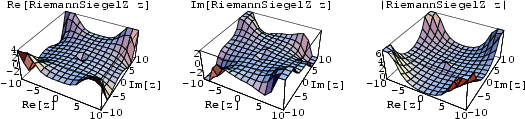
For a Real Positive ![]() , the Riemann-Siegel
, the Riemann-Siegel ![]() function is defined by
function is defined by
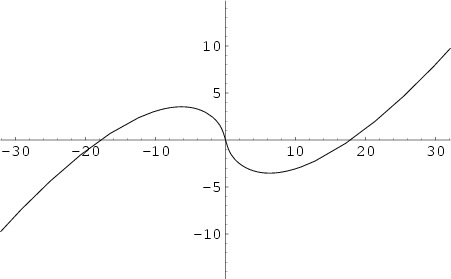

The Riemann-Siegel theta function appearing above is defined by
See also Riemann Zeta Function
References
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, p. 143, 1991.