Ramp Function

$$R(x) \equiv xH(x)$$ (1)

$$= \int^x_{-\infty} H(x')\,dx'$$ (2)

$$= \int_{-\infty}^\infty H(x')H(x-x')\,dx'$$ (3)

$$= H(x)*H(x),$$ (4)

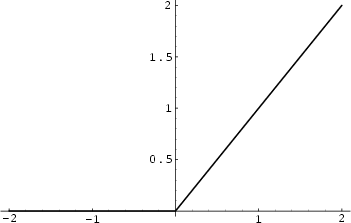
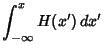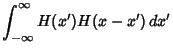where 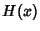$H(x)$ is the Heaviside Step Function and 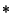$*$ is the Convolution. The Derivative is

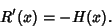$$R'(x) = -H(x).$$ (5)

The Fourier Transform of the ramp function is given by

$${\mathcal F}[R(x)]=\int_{-\infty}^\infty e^{-2\pi ikx}R(x)\,dx = \pi i\delta'(2\pi k)-{1\over 4\pi^2 k^2},$$ (6)

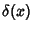where $\delta(x)$ is the Delta Function and 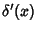$\delta'(x)$ its Derivative.

See also Fourier Transform--Ramp Function, Heaviside Step Function, Rectangle Function, Sgn, Square Wave