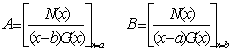2. 部分分式

任一既约真分式(分子与分母没有公因子，分子次数低于分母次数)都可唯一地分解成形如或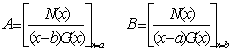的基本真分式之和，其运算称为部分分式展开.若为假分式(分子次数不低于分母次数)，应先化为整式与真分式之和，然后再对真分式进行部分分式展开.部分分式的各个系数可以通过待定系数法来确定.下面分几种不同情况介绍.

设

[线性因子重复]

1^o

式中N(x)的最高次数r≤m-1；A₀，A₁，L ，A_m-1为待定常数，可由下式确定：

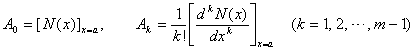
2^o

式中A₀，A₁，L ，A_m为待定常数，可由下式确定：

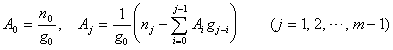
≤s-1

其系数f_j与m有关，由下表确定：

例

解 依上述公式算出

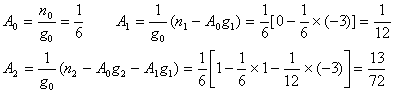
此时m=3，

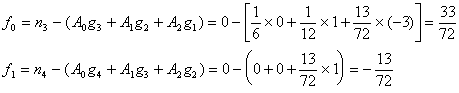
所以得到

3^o

作变换y=x-a，则N(x)=N₁(y), G(x)=G₁(y), 上式变为

用上述1^o，2^o的方法确定出A₀, A₁, L , A_m-1和F₁(y)，再将y=x-a代回.也可按下式来确定系数A₀, A₁, L , A_m-1：

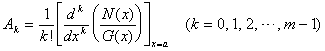
[线性因子不重复]

1^o

式中N(x)的最高次数r≤2，a¹ b¹ c；A, B, C为待定常数，可由下式确定：

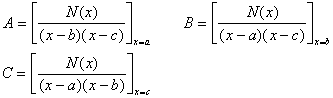
2^o

式中多项式F(x)的最高次数k≤s-1；A, B为待定常数，用下式确定：

A, B确定后，再用等式两边多项式同次项系数必须相等的法则来确定F(x)的各项系数.

例

解 依上述公式算得

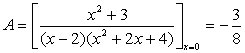
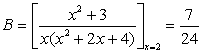
把A,B代入原式，通分并整理后得

比较等式两边同次项系数得

所以有

[高次因子]

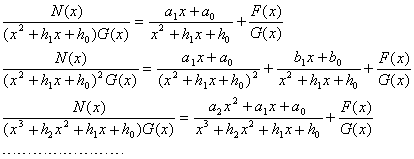
[计算系数的一般方法]

1^o 等式两边乘以D(x)化为整式，各项按x的同次幂合并，然后列出未知系数的方程组，解出而得.

2^o 等式两边乘以D(x)化为整式，再把x用简单的数值(如x=0, 1, -1等)代入，然后列出未知系数的方程组，解出而得.